2  Introduction to Time Series Analysis

The goal of this lecture is to introduce time series and their common components. You should become confident in identifying and characterizing trends, seasonal and other variability based on visual analysis of time series plots and plots of autocorrelation functions.

Objectives

1. Define time series, common components (decomposition), and patterns to look out for (outliers, change points, heteroskedasticity).
2. Distinguish simple models for univariate time series (building blocks for more complex models).
3. Define autocorrelation and partial autocorrelation and interpret such estimates.
4. Explain the assumption of stationarity for calculating autocorrelation.

Reading materials

• Chapters 1.1–1.4 in Brockwell and Davis (2002)

2.1 Time series and its components

‘A time series is a set of observations \(Y_t\), each one being recorded at a specific time \(t\)’ (Brockwell and Davis 2002). The index \(t\) will typically refer to some standard unit of time, e.g., seconds, hours, days, weeks, months, or years.

‘A time series is a collection of observations made sequentially through time’ (Chatfield 2000).

A stochastic process is a sequence of random variables \(Y_t\), \(t = 1, 2, \dots\) indexed by time \(t\), which can be written as \(Y_t\), \(t \in [1,T]\). A time series is a realization of a stochastic process.

We shall frequently use the term time series to mean both the data and the process.

Let’s try to describe the patterns we see in Figure 2.1, Figure 2.2, and Figure 2.3.

p <- forecast::autoplot(TSstudio::Michigan_CS) + 
    xlab("") + 
    ylab("Index")
plotly::ggplotly(p)

Figure 2.1: Monthly index of consumer sentiment, the University of Michigan Consumer Survey (1966:Q1 = 100).

ggplot2::autoplot(JohnsonJohnson) + 
    xlab("") + 
    ylab("Earnings per share (USD)")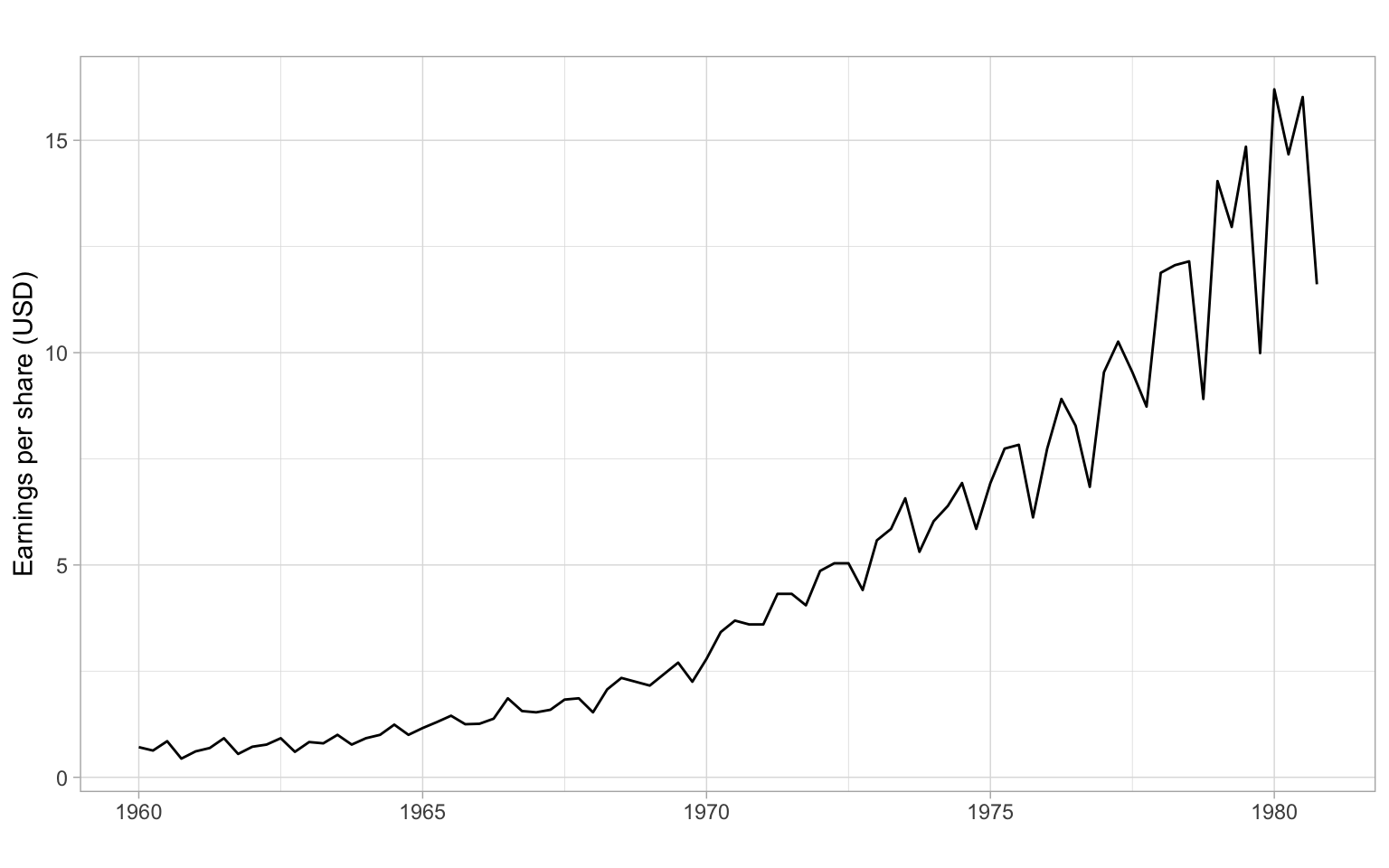

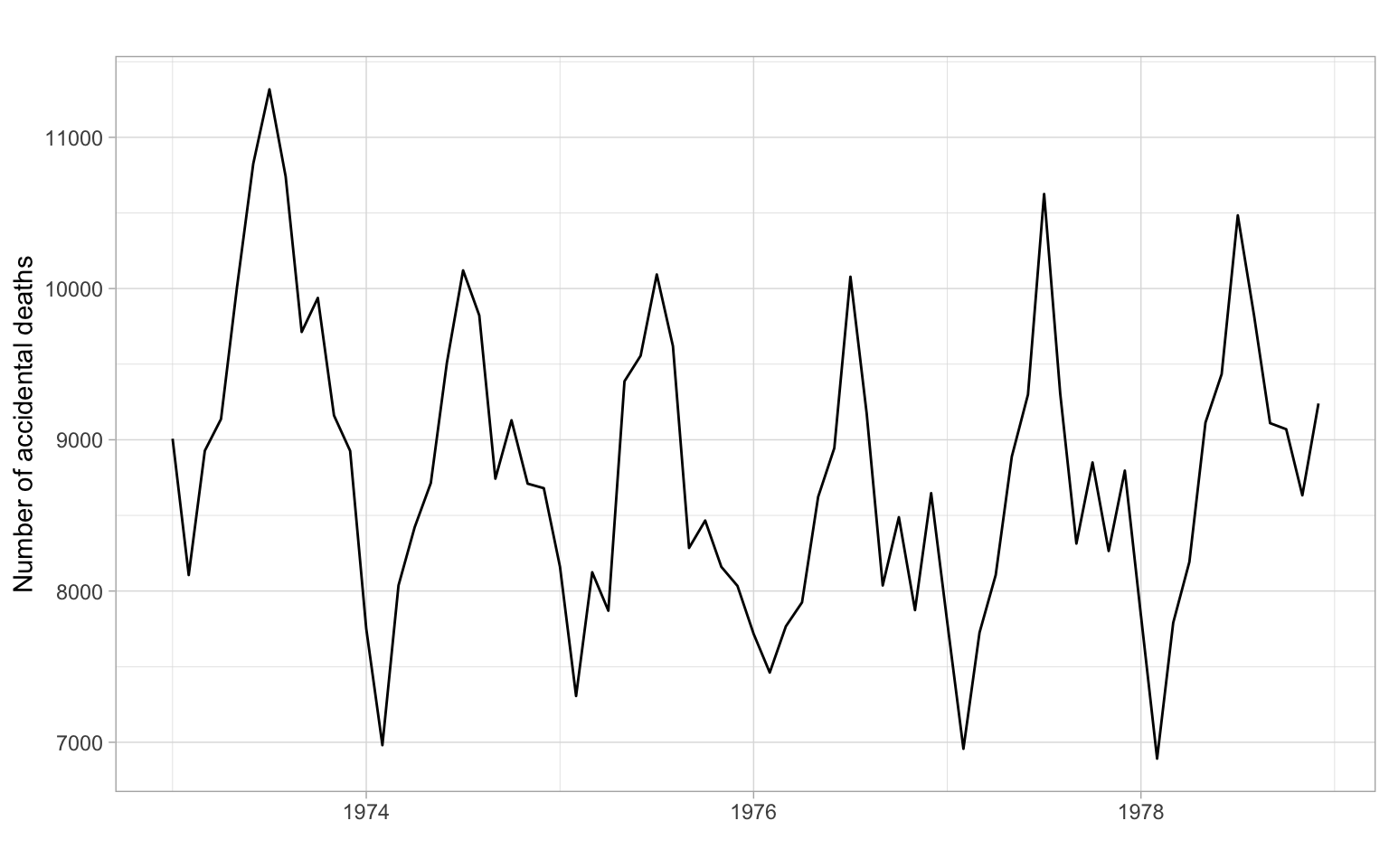
Figure 2.2: Quarterly earnings (dollars) per Johnson & Johnson share, 1960–1980.

ggplot2::autoplot(MASS::accdeaths) + 
    xlab("") + 
    ylab("Number of accidental deaths")

Figure 2.3: Monthly totals of accidental deaths in the USA, 1973–1978.

In this course, we will be interested in modeling time series to learn more about their properties and to forecast (predict) future values of \(Y_t\), i.e., values of \(Y_t\) for \(t\) beyond the end of the data set. Typically, we will use the historical data (or some appropriate subset of it) to build our forecasting models.

2.2 Decomposition of time series

A time series can generally be expressed as a sum or product of four distinct components: \[ Y_t = M_t + S_t + C_t + \epsilon_t \] or \[ Y_t = M_t \cdot S_t \cdot C_t \cdot \epsilon_t, \] where

1. \(M_t\) is the trend, representing the average change (change in the mean) in the time series over time. Examples of trends are:
   \(M_t = \beta_0\) (constant over time, we usually refer to this case as ‘no trend’);
   \(M_t = \beta_0 + \beta_1t\) (linear increase or decrease over time);
   \(M_t = \beta_0 + \beta_1t + \beta_2t^2\) (quadratic over time).
   
2. \(S_t\) represents regular periodic fluctuations (a.k.a. seasonality) in the time series. \(S_t\) has the property that it is not constant but there exists an integer \(m \geqslant 2\) and scaling factors \(\lambda_k > 0\) such that \(S_{t+km} = \lambda_kS_t\) for \(1 \leqslant t \leqslant m\) and each \(k \geqslant 1\). The smallest such \(m\) is called the period. Periodic time series are quite common and include seasonal variability (the period is 1 year), diurnal (the period is 24 hours), and other cycles such as tides (the period is 12 hours 25 minutes). This component can be modeled using sinusoidal functions or indicator variables.
3. \(C_t\) represents irregular cyclical fluctuations, i.e., sinusoidal-type movements that are of irregular length and are not as predictable as the seasonal component, e.g., El Niño Southern Oscillation (ENSO) and macroeconomic business cycles. We do not explicitly model \(C_t\) in this course.
4. \(\epsilon_t\) is the residual or error and represents the remaining unexplained variation in \(Y_t\). In other words, it is a random or stochastic component.

Figure 2.4 illustrates an automatic decomposition, however, because the user has too little control over how the decomposition is done, this function is not recommended. We will talk about the alternatives in the next lecture.

# births <- scan("http://robjhyndman.com/tsdldata/data/nybirths.dat")
births <- scan("data/nybirths.dat")
births <- ts(births, frequency = 12, start = c(1946, 1))
ggplot2::autoplot(decompose(births))

Figure 2.4: Time-series decomposition of the monthly number of births in New York City (thousands), 1946–1959.

2.3 General approach to time series modeling

1. Plot the series and examine the main features of the graph, checking whether there is
   • a trend,
   • a seasonal or another periodic component,
   • any apparent sharp changes in behavior,
   • any outlying observations.
2. Remove the trend and periodic components to get stationary residuals (this step is called detrending and deseasonalizing). Broadly speaking, a time series is said to be stationary if there is
   1. no systematic change in the mean (no trend),
   2. no systematic change in the variance, and
   3. no strictly periodic variations.
3. Choose a model to fit the residuals, making use of various sample statistics, including the sample autocorrelation function (ACF).
4. Forecast the residuals and then invert the transformations to arrive at forecasts of the original series.

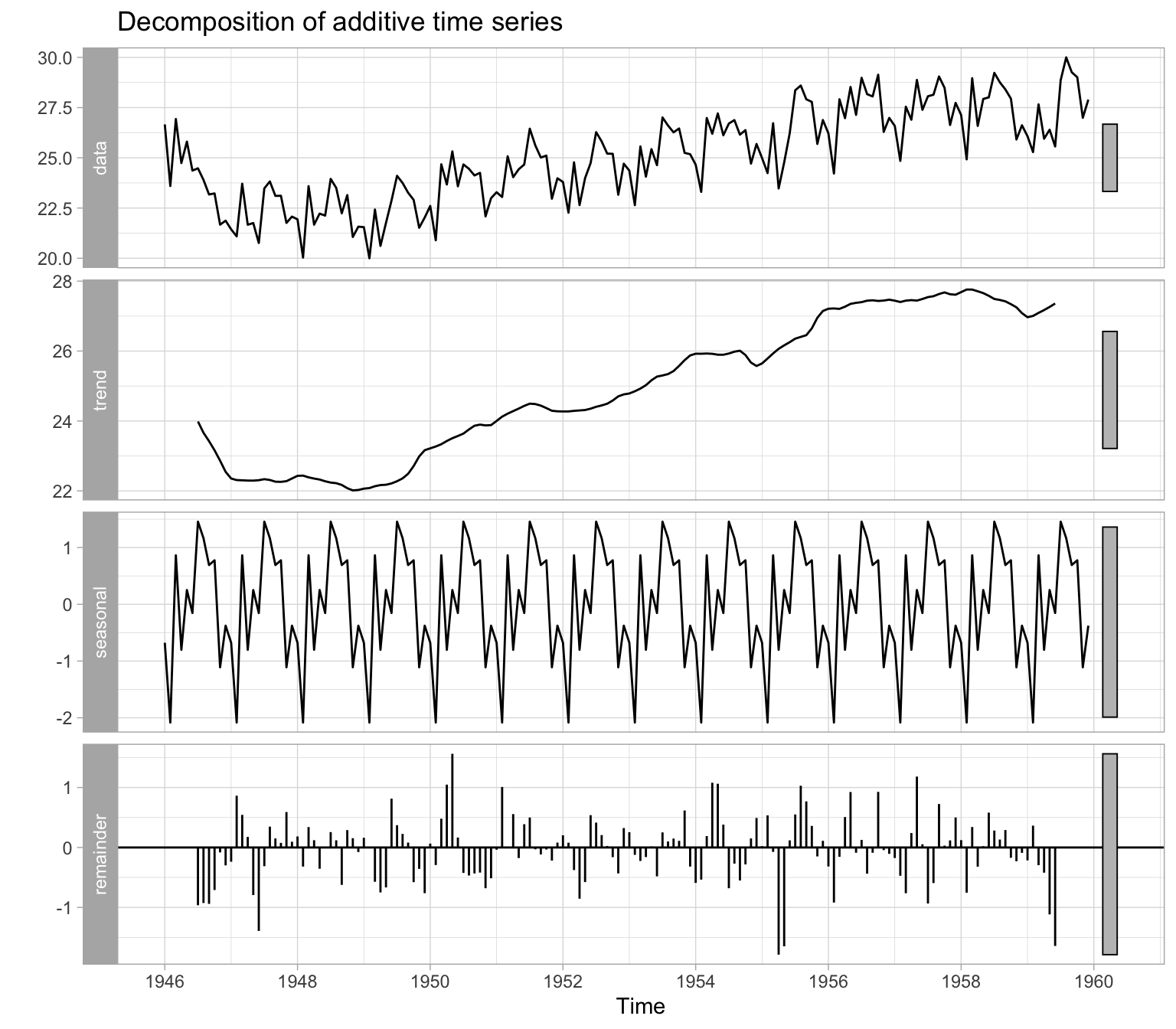
There are two general classes of forecasting models.

Univariate time series models include different types of exponential smoothing, trend models, autoregressive models, etc. The characteristic feature of these models is that we need only one time series to start with (\(Y_t\)), then we can build a regression of this time series over time (\(Y_t \sim t\)) for estimating the trend or, for example, an autoregressive model (‘auto’ \(=\) self). In the autoregressive approach, the current value \(Y_t\) is modeled as a function of the past values: \[ Y_t = f(Y_{t-1}, Y_{t-2}, \dots, Y_{t-p}) + \epsilon_t. \tag{2.1}\] A linear autoregressive model has the following form (assume that function \(f(\cdot)\) is a linear parametric function, with parameters \(\phi_0, \phi_1, \dots, \phi_p\)): \[ Y_t = \phi_0 + \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \dots +\phi_p Y_{t-p} + \epsilon_t. \]

Multivariate models involve additional covariates (a.k.a. regressors, predictors, or independent variables) \(X_{1,t}, X_{2,t}, \dots, X_{k,t}\). A multivariate time series model can be as simple as the multiple regression \[ Y_t = f(X_{1,t}, X_{2,t}, \dots, X_{k,t}) + \epsilon_t, \] or involve lagged values of the response and predictors: \[ \begin{split} Y_t = f(&X_{1,t}, X_{2,t}, \dots, X_{k,t}, \\ &X_{1,t-1}, X_{1,t-2}, \dots, X_{1,t-q1}, \\ &\dots\\ &X_{k,t-1}, X_{k,t-2}, \dots, X_{k,t-qk}, \\ &Y_{t-1}, Y_{t-2}, \dots, Y_{t-p}) + \epsilon_t, \end{split} \tag{2.2}\] where \(p\), \(q1, \dots, qk\) are the lags. We can start the analysis with many variables and build a forecasting model as complex as Equation 2.2, but remember that a simpler univariate model may also work well. We should create an appropriate univariate model (like in Equation 2.1) to serve as a baseline, then compare the models’ performance on some out-of-sample data, as described in Chapter 12.

Example: Identify the time-series components in these plots

ggplot2::autoplot(sunspots) + 
    xlab("") + 
    ylab("Sunspot number")

Figure 2.5: Monthly mean relative sunspot numbers from 1749 to 1983. Collected at Swiss Federal Observatory, Zurich until 1960, then Tokyo Astronomical Observatory. Notice the apparent periodicity, large variability when the series is at a high level, and small variability when the series is at a low level. This series is likely to have no trend over the time we have been able to observe it, though it may have a nearly perfectly periodic component.

ggplot2::autoplot(lynx) + 
    xlab("") + 
    ylab("Number of lynx trappings")

Figure 2.6: Annual numbers of lynx trappings for 1821–1934 in Canada. There is a clear cycle of about 10 years in length (the period is 10 years). There is potentially also a longer-term cycle.

ggplot2::autoplot(Nile) + 
    xlab("") + 
    ylab(bquote('Annual flow  '(10^8~m^3)))

Figure 2.7: Annual flow of the river Nile at Aswan, 1871–1970. There are signs of nonlinear dynamics or a changepoint.

ggplot2::autoplot(co2) + 
    xlab("") + 
    ylab(bquote(CO[2]~'concentration (ppm)'))

Figure 2.8: Monthly Mauna Loa atmospheric CO\(_2\) concentration, 1959–1997. There is a strong trend and a strong annual cycle.

ggplot2::autoplot(Ecdat::Consumption[,"yd"]/1000) + 
    xlab("") + 
    ylab("Income (thousand 1986 dollars)")

Figure 2.9: Quarterly personal disposable income (Canada, 1947–1996). There is a clear increasing trend of a relatively complex shape. Also, the variability increased in the later years.

forecast::autoplot(as.ts(Ecdat::SP500[,1])) + 
    xlab("") + 
    ylab("Daily return")

Figure 2.10: Daily returns (change in log index) on Standard & Poor’s 500 Index, 1981-01 to 1991-04. Business days are used as the time index to avoid data gaps during non-trading days. The mean and variance are constant overall (not increasing or decreasing), but there are clusters of volatility.

2.4 Some simple time series models

Recall that a random process is a sequence of random variables, so its model would be the joint distribution of these random variables \[ f_1(Y_{t_1}), \; f_2(Y_{t_1}, Y_{t_2}), \; f_3(Y_{t_1}, Y_{t_2}, Y_{t_3}), \dots \]

With sample data, usually, we cannot estimate so many parameters. Instead, we use only first- and second-order moments of the joint distributions, i.e., \(\mathrm{E}(Y_t)\) and \(\mathrm{E}(Y_tY_{t+h})\). In the case when all the joint distributions are multivariate normal (MVN), these second-order properties completely describe the sequence (we do not need any other information beyond the first two moments in this case).

• i.i.d. noise – independent and identically distributed random variables with zero mean. There is no dependence between observations, at any moment. The joint distribution function is \[ \Pr[Y_1\leqslant y_1, \dots, Y_n\leqslant y_n] = \Pr[Y_1\leqslant y_1]\dots \Pr[Y_n\leqslant y_n]. \] and the forecast is 0 (zero).
• binary process is a case of i.i.d. process with \(0 < p < 1\), and \[ \begin{split} \Pr[X_t=1]& = p, \\ \Pr[X_t=-1]& = 1-p. \end{split} \]
• random walk is a cumulative sum of i.i.d. noise: \[ S_t=X_1+X_2+\dots +X_t = \sum_{i=1}^t X_i, \] where \(t=1,2,\dots\), and \(X_t\) is i.i.d. noise.
• white noise (WN) is a sequence of uncorrelated random variables, each with zero mean and finite variance \(\sigma^2\). An i.i.d.(0,\(\sigma^2\)) series is also WN(0,\(\sigma^2\)), but not conversely.

2.5 Autocorrelation function

It is time to give more formal definitions of stationarity. Loosely speaking, a time series \(X_t\) (\(t=0,\pm 1, \dots\)) is stationary if it has statistical properties similar to those of the time-shifted series \(X_{t+h}\) for each integer \(h\).

Let \(X_t\) be a time series with \(\mathrm{E}(X^2_t)<\infty\), then the mean function of \(X_t\) is \[ \mu_X(t)=\mathrm{E}(X_t). \]

The autocovariance function of \(X_t\) is \[ \gamma_X(r,s) = \mathrm{cov}(X_r,X_s) = \mathrm{E}[(X_r-\mu_X(r))(X_s-\mu_X(s))] \tag{2.3}\] for all integers \(r\) and \(s\).

Weak stationarity

\(X_t\) is (weakly) stationary if \(\mu_X(t)\) is independent of \(t\), and \(\gamma_X(t+h,t)\) is independent of \(t\) for each \(h\) (consider only the first two moments): \[ \begin{split} \mathrm{E}(X_t) &= \mu, \\ \mathrm{cov}(X_t, X_{t+h}) &= \gamma_X(h) < \infty. \end{split} \tag{2.4}\]

Strong stationarity

\(X_t\) is strictly stationary if (\(X_1, \dots, X_n\)) and (\(X_{1+h}, \dots, X_{n+h}\)) have the same joint distribution (consider all moments).

Strictly stationary \(X_t\) with finite variance \(\mathrm{E}(X_t^2) <\infty\) for all \(t\) is also weakly stationary.

If \(X_t\) is a Gaussian process, then strict and weak stationarity are equivalent (i.e., one form of stationarity implies the other).

Note

In applications, it is usually very difficult if not impossible to verify strict stationarity. So in the vast majority of cases, we are satisfied with the weak stationarity. Moreover, we usually omit the word ‘weak’ and simply talk about stationarity (but have the weak stationary in mind).

Given the second condition of weak stationarity in Equation 2.4, we can write for stationary(!) time series the autocovariance function (ACVF) for the lag \(h\): \[ \gamma_X(h)= \gamma_X(t+h,t) = \mathrm{cov}(X_{t+h},X_t) \] and the autocorrelation function (ACF), which is the normalized autocovariance: \[ \rho_X(h)=\frac{\gamma_X(h)}{\gamma_X(0)}=\mathrm{cor}(X_{t+h},X_t). \]

The sample autocovariance function is defined as: \[ \hat{\gamma}_X(h)= n^{-1}\sum_{t=1}^{n-k}(x_{t+h}- \bar{x})(x_t - \bar{x}), \] with \(\hat{\gamma}_X(h) = \hat{\gamma}_X(-h)\) for \(h = 0,1,\dots, n-1\). In R, use acf(X, type = "covariance").

The sample autocorrelation function is defined as (in R, use acf(X)): \[ \hat{\rho}_X(h)=\frac{\hat{\gamma}_X(h)}{\hat{\gamma}_X(0)}. \]

2.5.1 Properties of autocovariance and autocorrelation functions

1. Linearity: if \(\mathrm{E}(X^2) < \infty\), \(\mathrm{E}(Y^2) < \infty\), \(\mathrm{E}(Z^2) < \infty\) and \(a\), \(b\), and \(c\) are any real constants, then \[ \mathrm{cov}(aX + bY + c, Z) = a\mathrm{cov}(X,Z) + b\mathrm{cov}(Y,Z). \]
2. \(\gamma(0) \geqslant 0\).
3. \(|\gamma(h)| \leqslant \gamma(0)\) for all \(h\).
4. \(\gamma(\cdot)\) is even: \(\gamma(h) = \gamma(-h)\) for all \(h\).
5. \(\gamma(\cdot)\) is nonnegative definite: \[ \sum_{i,j=1}^na_i \gamma(i-j)a_j\geqslant 0, \] for all positive integers \(n\) and vectors \(\boldsymbol{a} = (a_1, \dots, a_n)^{\top}\) with real-valued elements \(a_i\).
6. The autocorrelation function \(\rho(\cdot)\) has all the properties of autocovariance function plus \(\rho(0)=1\).
7. For i.i.d. noise with finite variance, the sample autocorrelations \(\hat{\rho}(h)\), \(h>0\), are approximately \(N(0,1/n)\) for large sample size \(n\). Hence, approximately 95% of the sample autocorrelations should fall between the bounds \(\pm1.96/\sqrt{n}\) (1.96 is the 0.975th quantile of the standard normal distribution) – this is the bound automatically drawn by the R function acf(). Autocorrelations that reach outside this bound are then statistically significant. Note that in R as a rule of thumb the default maximal lag is \(10 \log_{10}(n)\), and the same \(n\) is used for the confidence bounds at all lags (however, in reality, samples of different sizes are used for each lag).

Note

The last property is yet another tool for testing autocorrelation in a time series, in addition to those listed in Chapter 1. Also, see the Ljung–Box test described below.

Ljung–Box test

Instead of testing autocorrelation at each lag, we can apply an overall test by Ljung and Box (1978):

\(H_0\): \(\rho(1) = \rho(2) = \dots = \rho(h) = 0\)
\(H_1\): \(\rho(j) \neq 0\) for some \(j \in \{1, 2, \dots, h\}\), where \(n > h\).

The Ljung–Box test statistic is given by \[ Q_h = n(n + 2) \sum_{j = 1}^h\frac{\hat{\rho}_j^2}{n - j}. \] Under the null hypothesis, \(Q_h\) has a \(\chi^2\) distribution with \(h\) degrees of freedom. In R, this test is implemented in the function Box.test() with the argument type = "Ljung-Box" and in the function tsdiag().

Example: Compare ACFs of time series with and without a strong trend

The time series plot of births in Figure 2.11 shows a trend. The time series is not stationary. Thus, the calculated ACF is mostly useless (it is calculated under the assumption of stationarity), but we notice some periodicity in the ACF – it is a sign of periodicity in the time series itself (seasonality). Need to remove the trend (and seasonality) and repeat the ACF analysis.

Compare with the plots for accidental deaths in Figure 2.12.

p1 <- ggplot2::autoplot(births) + 
    xlab("") +
    ylab("Number of births (thousands)")
p2 <- forecast::ggAcf(births) + 
    ggtitle("") +
    xlab("Lag (months)")
p1 + p2 +
    plot_annotation(tag_levels = 'A')

Figure 2.11: Time series plot and sample ACF of the monthly number of births in New York City, 1946–1959.

p1 <- ggplot2::autoplot(MASS::accdeaths) + 
    xlab("") +
    ylab("Number of accidental deaths")
p2 <- forecast::ggAcf(MASS::accdeaths) + 
    ggtitle("") +
    xlab("Lag (months)")
p1 + p2 +
    plot_annotation(tag_levels = 'A')

Figure 2.12: Time series plot and sample ACF of monthly totals of accidental deaths in the USA, 1973–1978.

Figure 2.12 shows a slight trend of declining, then increasing deaths; the seasonal component in this time series is more dominant. The seasonal cycle of 12 months is clearly visible in the ACF.

Note

In base-R plots, the lags in ACF plots are measured in the number of periods. The period information (or frequency, i.e., the number of observations per period) is saved in the format ts in R:

is.ts(births)

#> [1] TRUE

frequency(births)

#> [1] 12

We don’t have to convert data to this format. If we plot the ACF of just a vector without these attributes, the values are the same, just the labels on the horizontal axis are different (Figure 2.13). For monthly data, as in the example here, the frequency is 12. Hence, here the ACF at lag 0.5 (Figure 2.13 A) means autocorrelation with the lag \(h=6\) months (Figure 2.13 B); lag 1 (Figure 2.13 A) corresponds to one whole period of \(h=12\) months (Figure 2.13 B), and so on.

par(mar = c(4, 4, 3, 1) + 0.1, mfrow = c(1, 2))

acf(births, lag.max = 37, las = 1, main = "A) Input is a ts object")
acf(as.numeric(births), lag.max = 37, las = 1, main = "B) Input is a numeric vector")

Figure 2.13: In base-R graphics, the x-axis labels in ACF plots differ depending on the input format.

Note

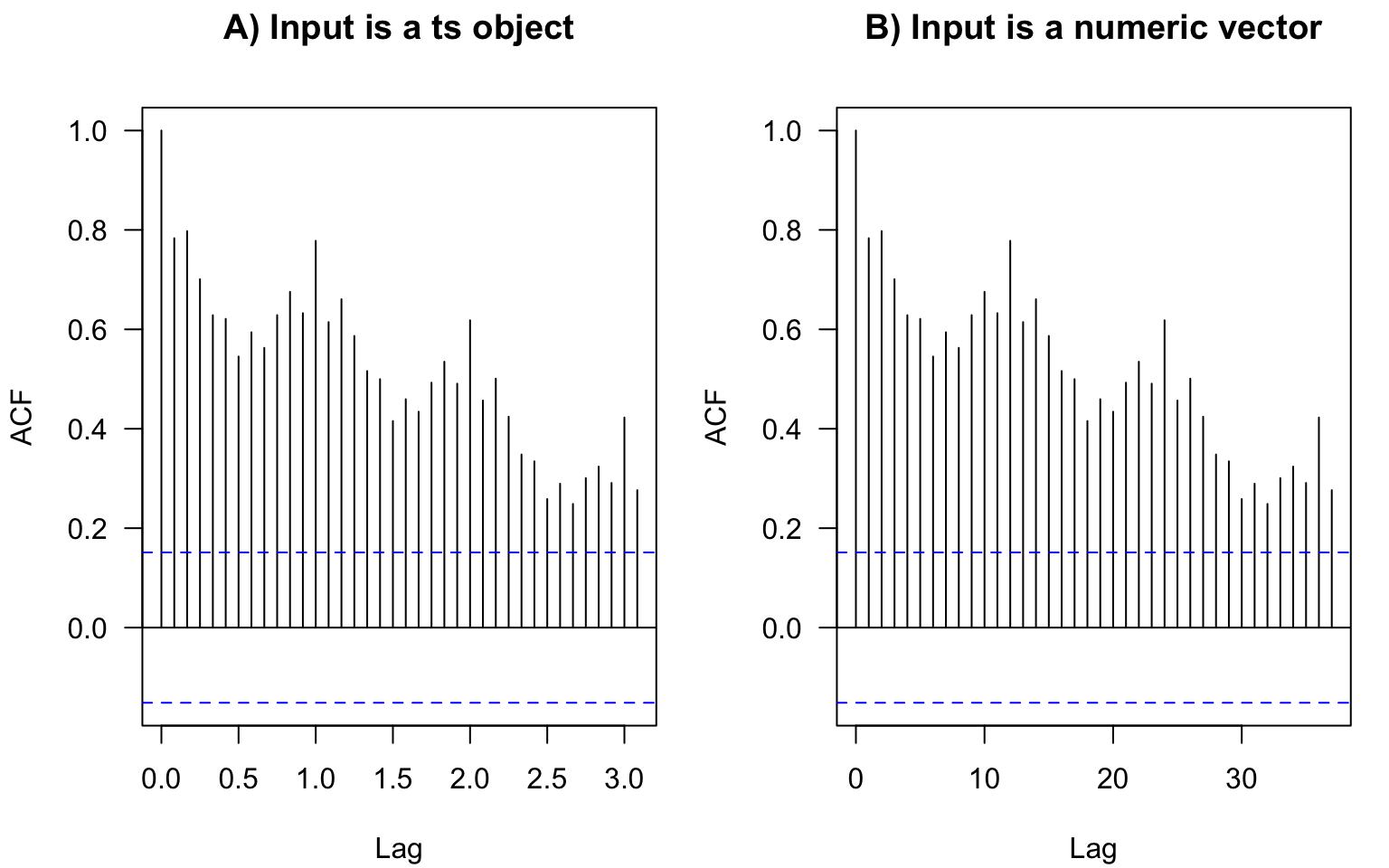
The ts objects in R cannot incorporate varying periods (e.g., different numbers of days or weeks because of leap years), therefore, we recommend using this format only for monthly or annual data. Setting frequency = 365.25 for daily data could be an option (although not very accurate) to accommodate leap years.

Converting to the ts format usually is not required for analysis. Most of the time we use plain numeric vectors and data frames in R.

Contributed R packages offer additional formats for time series, e.g., see the packages xts and zoo.

ACF measures the correlation between \(X_t\) and \(X_{t+h}\). The correlation can be due to a direct connection or through the intermediate steps \(X_{t+1}, X_{t+2}, \dots, X_{t+h-1}\). Partial ACF looks at the correlation between \(X_t\) and \(X_{t+h}\) once the effect of intermediate steps is removed.

2.6 Partial autocorrelation function

Shumway and Stoffer (2011) and Shumway and Stoffer (2014) provide the following explanation of the concept.

Recall that if \(X\), \(Y\), and \(Z\) are random variables, then the partial correlation between \(X\) and \(Y\) given \(Z\) is obtained by regressing \(X\) on \(Z\) to obtain \(\hat{X}\), regressing \(Y\) on \(Z\) to obtain \(\hat{Y}\), and then calculating \[ \rho_{XY|Z} = \mathrm{cor}(X - \hat{X}, Y - \hat{Y}). \] The idea is that \(\rho_{XY|Z}\) measures the correlation between \(X\) and \(Y\) with the linear effect of \(Z\) removed (or partialled out). If the variables are multivariate normal, then this definition coincides with \(\rho_{XY|Z} = \mathrm{cor}(X,Y | Z)\).

The partial autocorrelation function (PACF) of a stationary process, \(X_t\), denoted \(\rho_{hh}\), for \(h = 1,2,\dots\), is \[ \rho_{11} = \mathrm{cor}(X_t, X_{t+1}) = \rho(1) \] and \[ \rho_{hh} = \mathrm{cor}(X_t - \hat{X}_t, X_{t+h} - \hat{X}_{t+h}), \; h\geqslant 2. \]

Both \((X_t - \hat{X}_t)\) and \((X_{t+h} - \hat{X}_{t+h})\) are uncorrelated with \(\{ X_{t+1}, \dots, X_{t+h-1}\}\). The PACF, \(\rho_{hh}\), is the correlation between \(X_{t+h}\) and \(X_t\) with the linear dependence of everything between them (intermediate lags), namely \(\{ X_{t+1}, \dots, X_{t+h-1}\}\), on each, removed.

In other notations, the PACF for the lag \(h\) and predictions \(P\) is \[ \rho_{hh} = \begin{cases} 1 & \text{if } h = 0 \\ \mathrm{cor}(X_t, X_{t+1}) = \rho(1) & \text{if } h = 1 \\ \mathrm{cor}(X_t - P(X_t | X_{t+1}, \dots, X_{t+h-1}), \\ \quad\;\; X_{t+h} - P(X_{t+h} | X_{t+1}, \dots, X_{t+h-1})) & \text{if } h > 1. \end{cases} \]

To obtain sample estimates of PACF in R, use pacf(X) or acf(X, type = "partial").

Correlation and partial correlation coefficients measure the strength and direction of the relationship, changing within \([-1, 1]\). The percent of explained variance for the case of two variables is measured by squared correlation (r-squared; \(R^2\); coefficient of determination) changing within \([0, 1]\), so a correlation of 0.2 means only 4% of variance explained by the simple linear relationship (regression). To report a partial correlation, for example, of 0.2 at lag 3, one could say something like ‘The partial autocorrelation at lag 3 (after removing the influence of the intermediate lags 1 and 2) is 0.2’ (depending on the application, the correlation of 0.2 can be considered weak or moderate strength) or ‘After accounting for autocorrelation at intermediate lags 1 and 2, the linear relationship at lag 3 can explain 4% of the remaining variability.’

The partial autocorrelation coefficients of i.i.d. time series are asymptotically distributed as \(N(0,1/n)\). Hence, for lags \(h > p\), where \(p\) is the optimal or true order of the partial autocorrelation, \(\rho_{hh} < 1.96/\sqrt{n}\) (assuming the confidence level 95%). This suggests using as a preliminary estimator of the order \(p\) the smallest value \(m\) such that \(\rho_{hh} < 1.96/\sqrt{n}\) for \(h > m\).

Example: ACF and PACF of accdeaths

By plotting ACF and PACF (Figure 2.14), we observe that most of the temporal dependence (autocorrelation) in this time series is due to correlation with the immediately preceding values (see PACF at lag 1).

p1 <- forecast::ggAcf(MASS::accdeaths) + 
    ggtitle("") +
    xlab("Lag (months)")
p2 <- forecast::ggAcf(MASS::accdeaths, type = "partial") + 
    ggtitle("") +
    xlab("Lag (months)")
p1 + p2 +
    plot_annotation(tag_levels = 'A')

Figure 2.14: ACF and PACF plots of the monthly accidental deaths.

2.7 Conclusion

We have defined components of the time series including trend, periodic component, and unexplained variability (errors, residuals). Our goal will be to model trends and periodicity, extract them from the time series, then extract as much information as possible from the remainder, so the ultimate residuals become white noise.

White noise is a sequence of uncorrelated random variables with zero mean and finite variance. White noise is also an example of a weakly stationary time series. The i.i.d. noise is strictly stationary (all moments of the distribution stay identical through time), and i.i.d. noise with finite variance is also white noise.

Time-series dependence can be quantified using a (partial) autocorrelation function. We defined (P)ACF for stationary series; R functions also assume stationarity of the time series when calculating ACF or PACF.

After developing several models for modeling and forecasting time series, we can compare them quantitatively in cross-validation. For time series, it is typical to have the testing set (or a validation fold) to be after the training set. Models can be compared based on the accuracy of their point forecasts and interval forecasts.

Brockwell PJ, Davis RA (2002) Introduction to time series and forecasting, 2nd edn. Springer, New York, NY, USA

Chatfield C (2000) Time-series forecasting. CRC Press, Boca Raton, FL, USA

Ljung GM, Box GEP (1978) On a measure of lack of fit in time series models. Biometrika 65:297–303. https://doi.org/10.1093/biomet/65.2.297

Shumway RH, Stoffer DS (2011) Time series analysis and its applications with R examples, 3rd edn. Springer, New York, NY, USA

Shumway RH, Stoffer DS (2014) Time series analysis and its applications with R examples, 3-EZ. Free Texts in Statistics