Advanced Semi-Supervised Learning With Uncertainty Estimation for Phase Identification in Distribution Systems
Citation (IEEE)
K. Kumar, K. Utkarsh, J. Wang, and H. V. Padullaparti, “Advanced Semi-Supervised Learning With Uncertainty Estimation for Phase Identification in Distribution Systems,” Proc. IEEE Power & Energy Society General Meeting (PESGM), 2025.
Abstract
The integration of advanced metering infrastructure (AMI) into power distribution networks generates valuable data for tasks such as phase identification; however, the limited and unreliable availability of labeled data in the form of customer phase connectivity presents challenges. To address this issue, we propose a semi-supervised learning (SSL) bayesian framework that effectively leverages both limited labeled and unlimited unlabeled data.
- Why Phase Identification Needs a New Approach ?
Problem: Utilities don’t know which phase customers are connected to this affects voltage regulation, DER integration, and fault localization.
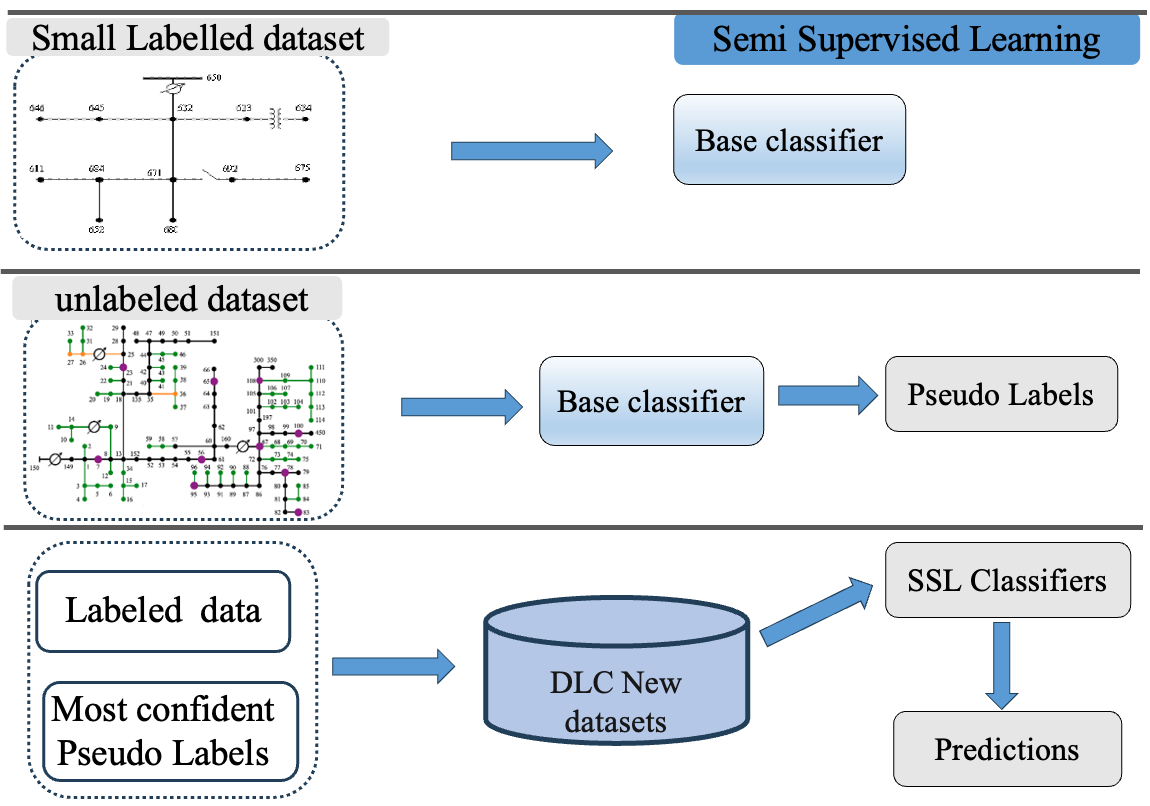
Fig. 1: Illustration of Semi-Supervised Learning Techniques
|
Challenges & Motivation
|
Contribution
Our approach incorporates:
- Self-training with an ensemble of multilayer perceptron classifiers.
- Label spreading to propagate labels based on data similarity.
- Bayesian Neural Networks (BNNs) for uncertainty estimation, improving confidence and reducing phase identification errors.
Key Highlights:*
- Achieved ~98% ± 0.08 accuracy on real utility data (Duquesne Light Company) using minimal and unreliable labeled data.
- Uncertainty-aware predictions reduce misclassification risk and improve smart grid reliability.
- Combines pseudo-labeling, graph-based SSL, and probabilistic modeling to handle data scarcity in real-world distribution networks.
Our “SSL + Uncertainty Estimation” approach provides an efficient and scalable solution for phase identification in AMI data, enabling utilities to improve modeling, simulation, and operational decision-making.
3. Problem Formulation of Framework for AMI
We define phase identification as a semi-supervised classification problem,\@ref(eq:black-scholes2) where the dataset \(D = D_L \cup D_U\) consists of a small labeled subset \(D_L\) and a large unlabeled subset \(D_U\).
The SSL objective is a regularized minimization:
\[ \min_{f \in \mathcal{F}} \left[ \frac{1}{n_L} \sum_{i=1}^{n_L} \ell(f(x_i), y_i) + \lambda R(f, \mathcal{D}_U) \right] \]{#eq:black-scholes2}
where:
- \(\ell\) is the supervised loss (e.g., cross-entropy)
- \(R(f, \mathcal{D}_U)\) is the regularization term capturing structure in the unlabeled data, - \(\lambda\) : trade-off parameter controlling the influence of unlabeled data
This formulation encourages the model to learn a decision boundary consistent with both labeled examples and the structure of the unlabeled feature space. c’
Methodology
4.1 Self-Training with MLP Ensembles
The MLP classifier f(x; \(\theta\)) is trained on \(D_L\) to minimize cross-entropy loss (Equation 1):
\[ \theta = \arg\min_\theta \sum_{(x_i, y_i) \in D_L} \mathcal{L}(f(x_i; \theta), y_i) \tag{1}\]
Unlabeled samples with high prediction confidence \(p_j\) > \(\tau\) receive pseudo-labels:
\[ D^{\text{new}}_L = \{(x_j, \hat{y}_j) \mid p_j > \tau\} \]
The process repeats iteratively, enriching the labeled dataset.
4.2 Label Spreading (Graph-Based SSL)
We construct a similarity matrix \(W\) where edge weights encode feature similarity:
\[ W_{ij} = \begin{cases} \exp\!\left(-\frac{\|x_i - x_j\|^2}{\sigma^2}\right), & i \neq j \\ 0, & i = j \end{cases} \]
Label distributions are updated iteratively as:
\[ Y^{(t+1)} = (1 - \alpha)Y^{(t)} + \alpha D^{-1}WY^{(t)} \]
This propagates known labels through the data manifold, smoothing class boundaries.
4.3 Bayesian Neural Networks (BNNs)
BNNs treat weights as random variables, assigning a Gaussian prior:
\[ p(W) = \mathcal{N}(W | \mu_{W}, \sigma_W^2) \]
Given training data \(D_L\), the posterior distribution is:
\[ p(W | D_L) \propto p(D_L | W) \, p(W) \]
The predictive distribution integrates over all possible weight configurations:
\[ p(y^* | x^*, D_L) = \int p(y^* | x^*, W) \, p(W | D_L) \, dW \]
We approximate this via Monte Carlo dropout by averaging multiple stochastic forward passes:
\[ \hat{y}^* = \frac{1}{N} \sum_{n=1}^N f(x^*; W_n) \] ### 4.4 Uncertainty Quantification
Two forms of uncertainty are estimated:
Epistemic (Model Uncertainty): \[ U_{\text{epistemic}} = \mathrm{Var}(\hat{y}^*) \]
Aleatoric (Data Uncertainty): \[ U_{\text{aleatoric}} = \mathbb{E}\!\left[(\hat{y}^* - \mathbb{E}[\hat{y}^*])^2\right] \]
Together, they help distinguish between what the model doesn’t know and what cannot be known due to noise.
5. Experimental Framework
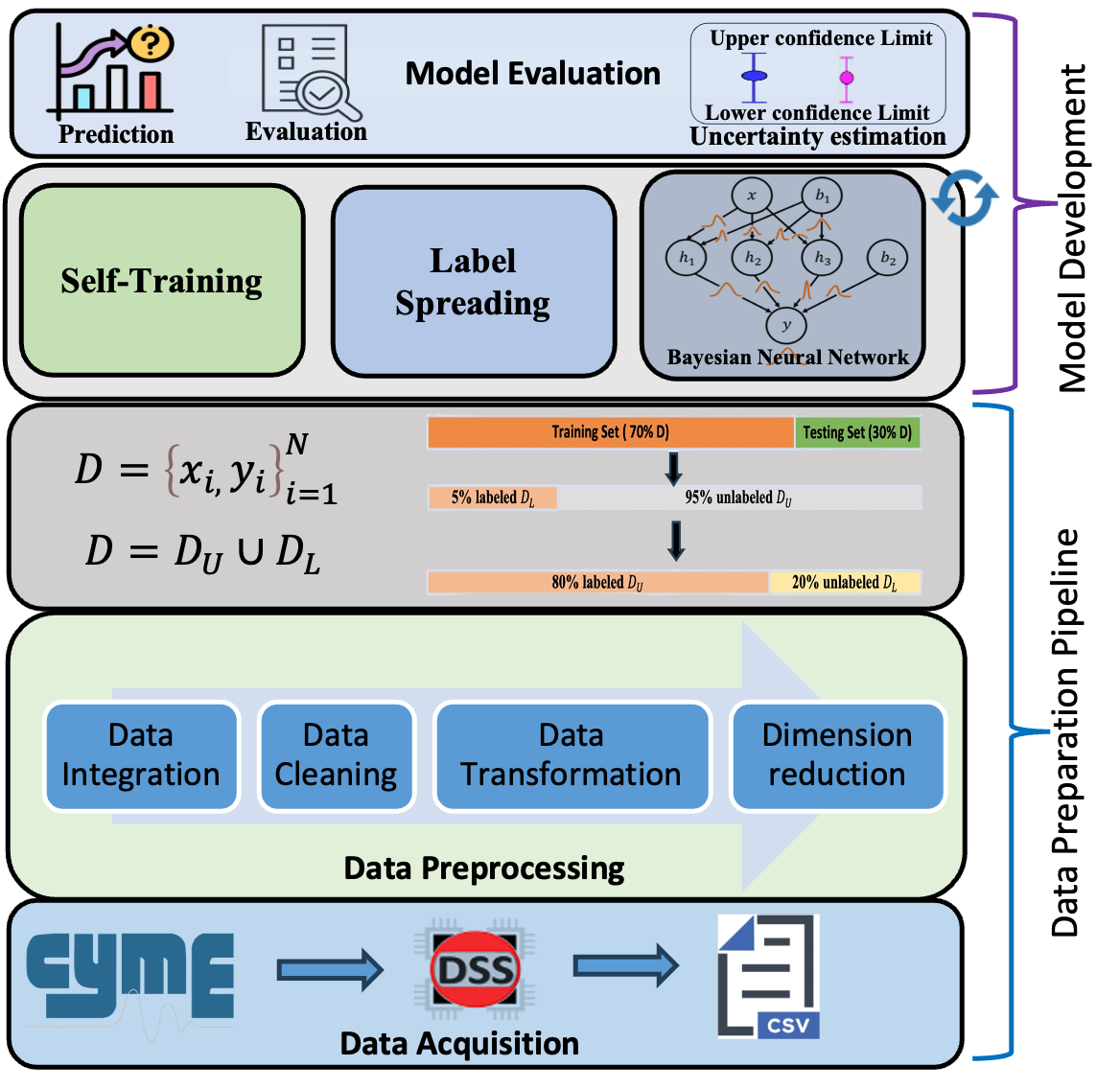
Data Flow and Setup
- Dataset Source: Real AMI data from a U.S. utility (Duquesne Light Company).
- Feature Set:
( F = {R_0, X_0, R_1, X_1, P, V_{}, V_{}, V_{}} )
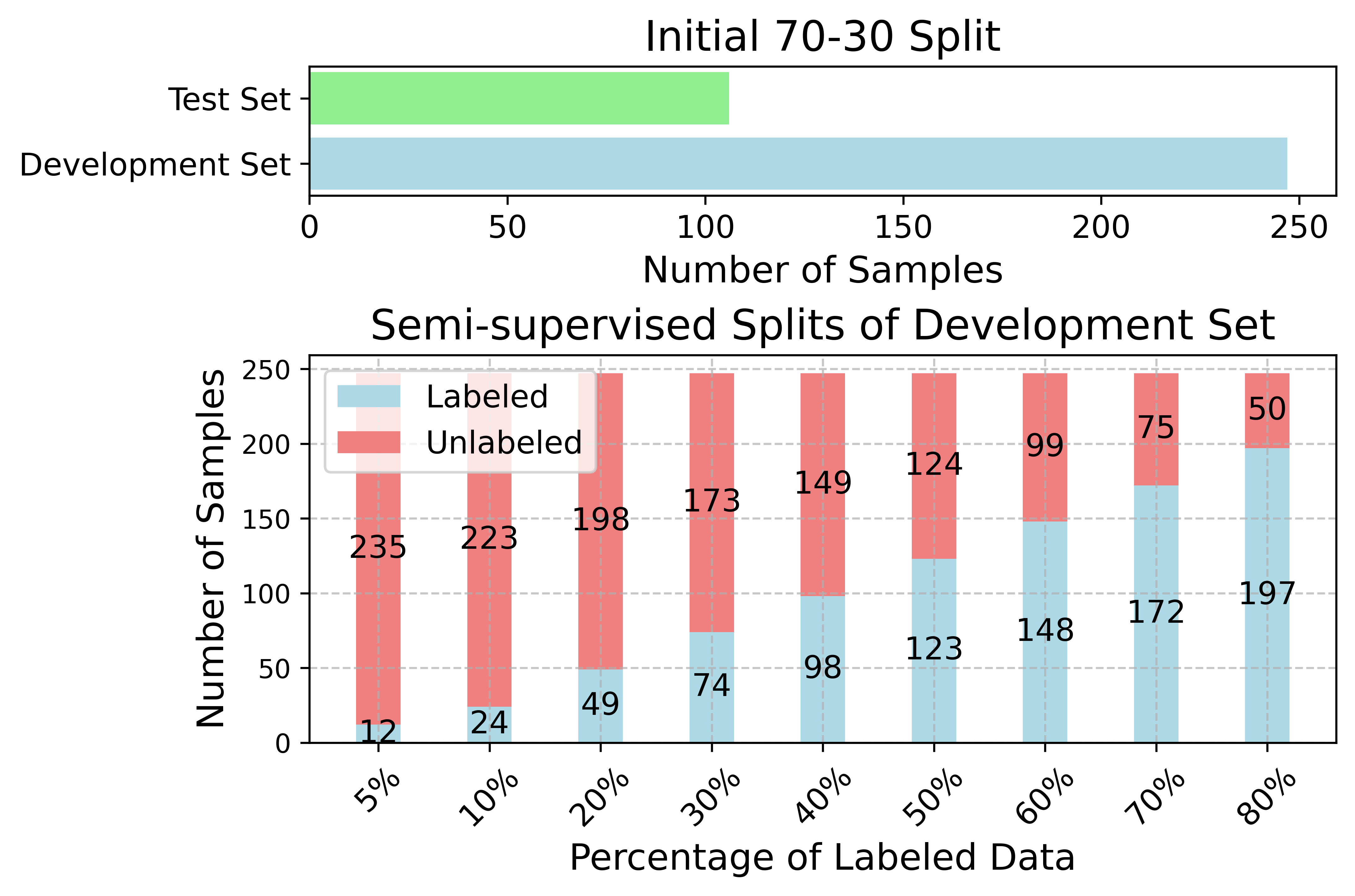
- Data Split: 70% development, 30% test; within development, labeled fractions vary from 5–80%.
- Models:
- MLP (64–32 layers, ReLU activation)
- Label Spreading with kNN kernel
- 3-layer BNN using Gaussian priors, dropout rate 0.7, Adam optimizer
- MLP (64–32 layers, ReLU activation)
6. Results and Discussion
BNNs outperformed both self-training and label spreading across all labeled data ratios.
When only 5% of the dataset was labeled, BNNs already achieved 64.15% ± 0.14, compared to 34.9% for self-training and 44.3% for label spreading.
At 70% labeled data, the BNN reached 99.06% ± 0.06 accuracy.
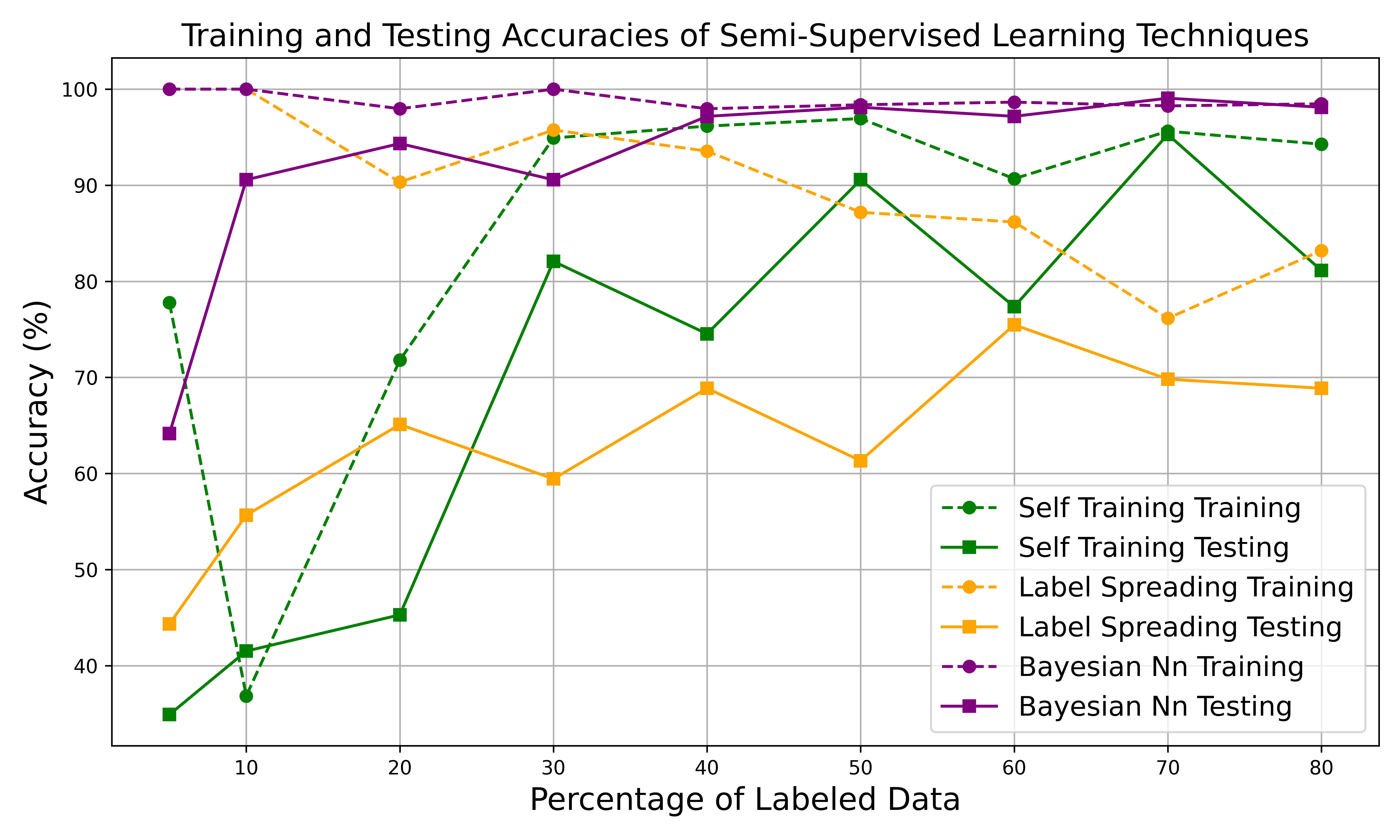
Interpretation:
BNNs’ probabilistic nature allows them to express how sure they are about each decision. This prevents overfitting and enables informed decision-making when data are uncertain—crucial for utility operations.
7. Conclusion
This research presents a semi-supervised learning framework enhanced with Bayesian uncertainty estimation for phase identification in power distribution systems.
By integrating pseudo-labeling, graph-based label propagation, and Bayesian inference, our framework achieves robust performance with minimal labeled data—98% ± 0.08 accuracy—and provides confidence metrics for each prediction.
This uncertainty-aware paradigm is a step toward trustworthy, data-efficient, and intelligent smart grids, where models not only predict but also know when they might be wrong.
- Proposed SSL Framework Applied to AMI Data

- Distribution Feeder Topology

- Training and Testing Data Partitions

- Accuracy Comparison of SSL Methods
