Advanced Semi-Supervised Learning With Uncertainty Estimation for Phase Identification in Distribution Systems
Citation (IEEE)
K. Kumar, K. Utkarsh, J. Wang, and H. V. Padullaparti, “Advanced Semi-Supervised Learning With Uncertainty Estimation for Phase Identification in Distribution Systems,” Proc. IEEE Power & Energy Society General Meeting (PESGM), 2025.
Abstract
The integration of advanced metering infrastructure (AMI) into power distribution networks generates valuable data for tasks such as phase identification; however, the limited and unreliable availability of labeled data in the form of customer phase connectivity presents challenges. To address this issue, we propose a semi-supervised learning (SSL) framework that effectively leverages both labeled and unlabeled data.
- Why Phase Identification Needs a New Approach ?
Problem: Utilities don’t know which phase customers are connected to — this affects voltage regulation, DER integration, and fault localization. • Challenge: Ground truth phase data is scarce, unreliable, and costly to collect. • Supervised learning ML methods need lots of labeled data – often unavailable or unreliable. • Motivation: How do we scale phase identification without needing tons of labeled data?
add techniques
Contribution
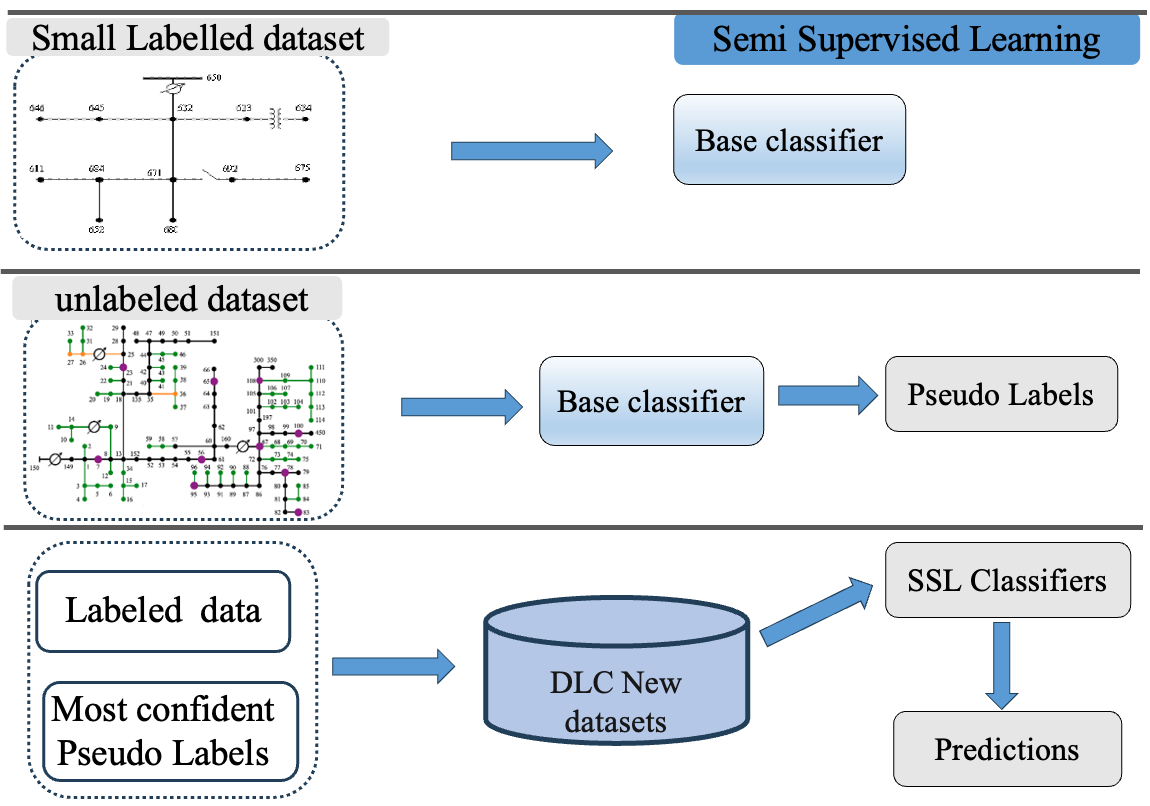
Our approach incorporates:
- Self-training with an ensemble of multilayer perceptron classifiers.
- Label spreading to propagate labels based on data similarity.
- Bayesian Neural Networks (BNNs) for uncertainty estimation, improving confidence and reducing phase identification errors.
Key Highlights:
- Achieved ~98% ± 0.08 accuracy on real utility data (Duquesne Light Company) using minimal and unreliable labeled data.
- Uncertainty-aware predictions reduce misclassification risk and improve smart grid reliability.
- Combines pseudo-labeling, graph-based SSL, and probabilistic modeling to handle data scarcity in real-world distribution networks.
Our SSL + Uncertainty Estimation approach provides an efficient and scalable solution for phase identification in AMI data, enabling utilities to improve modeling, simulation, and operational decision-making.
Semi-Supervised Learning Framework
We formulate SSL as a regularized optimization problem:Equation 1
\[ \min_{f \in \mathcal{F}} \left[ \frac{1}{n_L} \sum_{i=1}^{n_L} \ell(f(x_i), y_i) + \lambda R_u(f, \mathcal{D}_U) \right] \tag{1}\]
Where:
- ( (, ) ): Supervised loss (cross-entropy)
- ( R_u(f, _U) ): Unsupervised regularization term
- ( ): Trade-off parameter
The challenge is designing ( R_u(f, _U) ) to effectively leverage unlabeled data.
\[\begin{equation}
f\left(k\right) = \binom{n}{k} p^k\left(1-p\right)^{n-k}
(\#eq:binom)
\end{equation}\] You may refer to using \@ref(eq:binom), like see Equation @ref(eq:binom).
We formulate SSL as a regularized optimization problem:
\[ \min_{f \in \mathcal{F}} \left[ \frac{1}{n_L} \sum_{i=1}^{n_L} \ell(f(x_i), y_i) + \lambda R_u(f, \mathcal{D}_U) \right] \] Where \[a^2 + b^2 = d^2\] is the Unsupervised regularization term
Where: \[
R_u(f, \mathcal{D}_U)
\] is the - ( (, ) ): Supervised loss (cross-entropy)
- ( R_u(f, _U) ): Unsupervised regularization term
- ( ): Trade-off parameter
The challenge is designing ( R_u(f, _U) ) to effectively leverage unlabeled data.
\[\ell(\cdot, \cdot)\]: Supervised loss (cross-entropy)
\[R_u(f, \mathcal{D}_U)\]: Unsupervised regularization term
\[\lambda\]: Trade-off parameter
( (, ) ): Supervised loss (cross-entropy)
( R_u(f, _U) ): Unsupervised regularization term
( ): Trade-off parameter
We formulate SSL as a regularized optimization problem: min_{f∈ℱ} [ (1/n_L) ∑^{n_L}_{i=1} ℓ(f(x_i), y_i) + λR_u(f, 𝒟_U) ] Where:
ℓ(·,·): Supervised loss (cross-entropy) R_u(f, 𝒟_U): Unsupervised regularization term λ: Trade-off parameter
The challenge: designing R_u(f, 𝒟_U) that effectively exploits unlabeled data structure ## Methodology
We define the binomial distribution as:(Equation 2)
\[ f(k) = \binom{n}{k} p^k (1-p)^{n-k} \tag{2}\]
As shown in Equation @ref(eq:binom), the binomial function defines the probability…
Black-Scholes (Equation 3) is a mathematical model that seeks to explain the behavior of financial derivatives, most commonly options:
\[ \frac{\partial \mathrm C}{ \partial \mathrm t } + \frac{1}{2}\sigma^{2} \mathrm S^{2} \frac{\partial^{2} \mathrm C}{\partial \mathrm S^2} + \mathrm r \mathrm S \frac{\partial \mathrm C}{\partial \mathrm S}\ = \mathrm r \mathrm C \tag{3}\]
- Proposed SSL Framework Applied to AMI Data
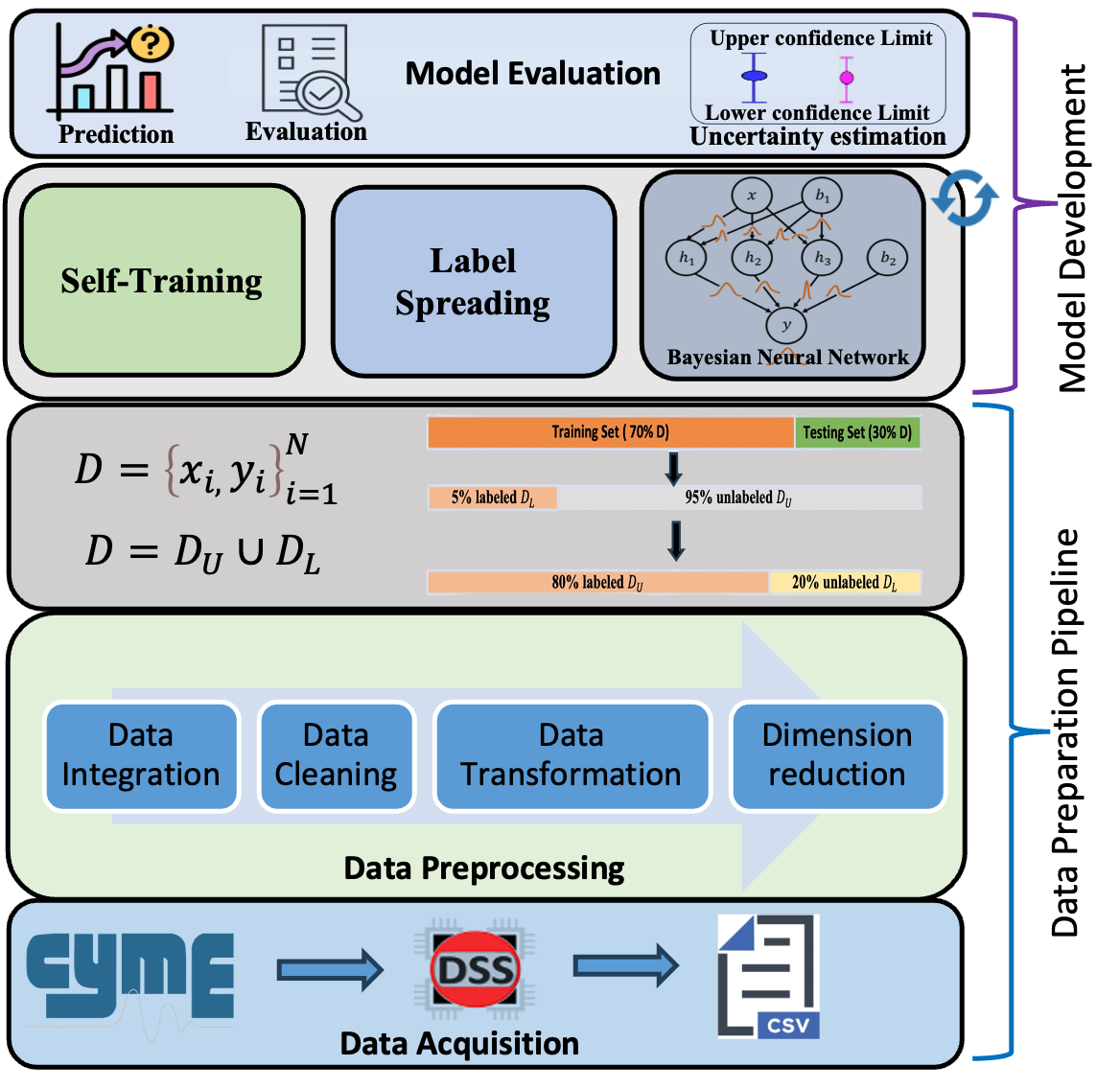
- Distribution Feeder Topology
- Training and Testing Data Partitions
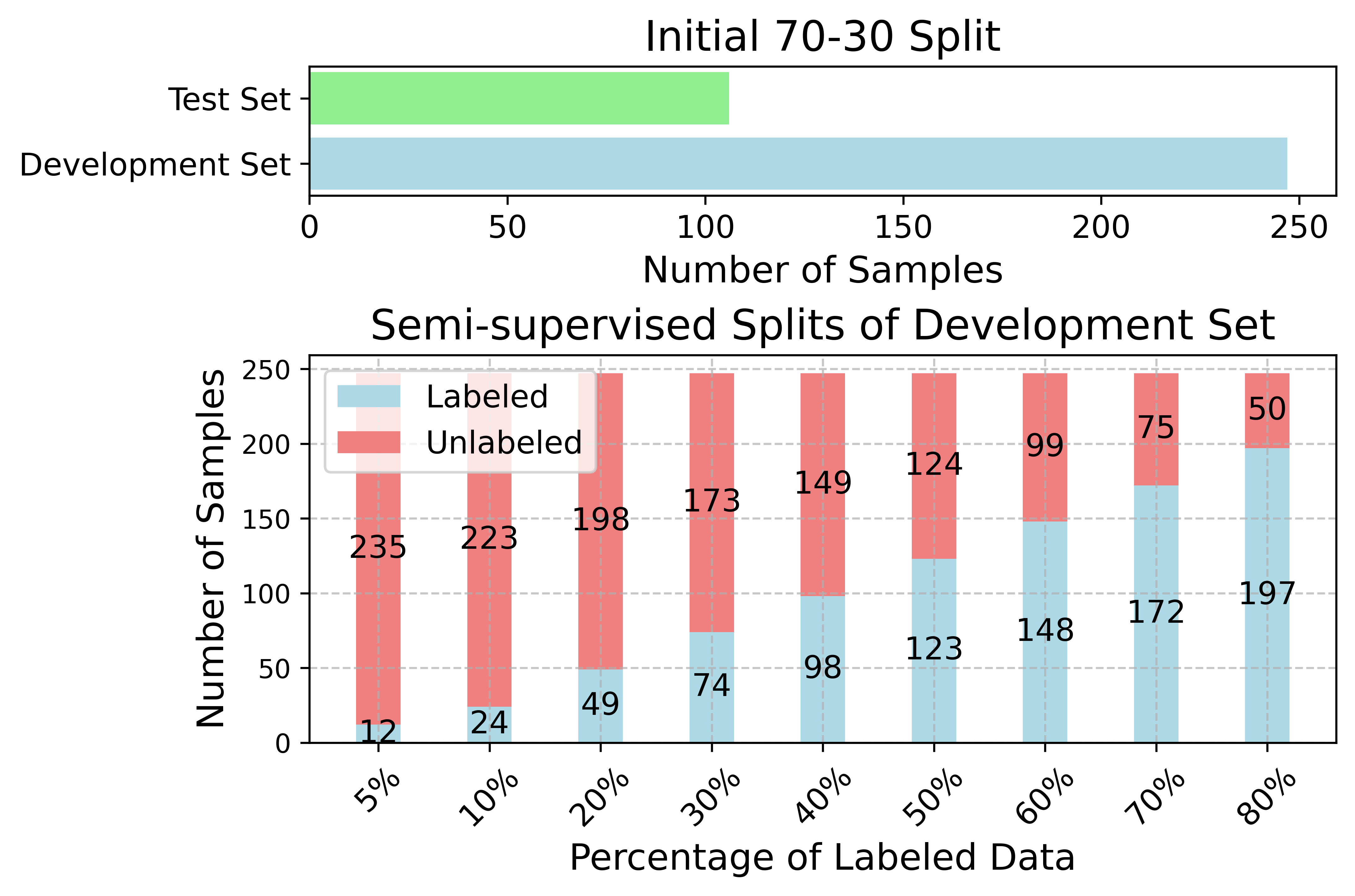
- Accuracy Comparison of SSL Methods